Что такое производная функции, интеграл, первообразная функции? Математика для гуманитариев

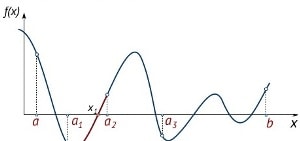
Чтобы понять, что такое производная, первообразная и интеграл, необходимо разобраться в том, что такое функция.

Существует несколько разделов математики, одним из которых является арифметика. Арифметика работает с множеством чисел -  натуральных (числа, которые используются при нумерации реальных предметов – первое дерево, второе дерево, третье дерево и т.д. и при подсчете их числа – ноль яблок, три яблока и т.д.), рациональных (дробные) и других видов чисел, а также занимается операциями сложения, вычитания, умножения и деления этих чисел. Однако арифметика всегда работает только с числами. Когда появляется необходимость увидеть характер отношений между числами, но не сами числа, возникает алгебра. Здесь числа обозначаются буквами (х, у и т.д.). Когда необходимо понять, как, например, при соотношении х+у будут вести себя числа, подставленные в места, где были буквы, подсчитывают уравнение и строят график, который показывает, как числа ряда х зависят от чисел ряда у. Саму зависимость при этом называют функцией. Почему функцией? Потому что она описывает, как будут вести себя все числа, подставленные в уравнение и не важно, какими будут эти числа. По существу, график – не есть сама функция, но лишь ее визуальное отображение. Таким образом, функция – это закон, который гласит, что чем меньше пончиков ты съешь (аргумент 1) и чем больше будешь при этом заниматься спортом (аргумент 2), тем быстрее сбросишь лишний вес (результат функции). В этом примере скорость избавления от лишнего веса будет являться функцией, описывающей следствия занятия спортом и отказа от пончиков.

Рассмотрим на абстрактном примере. Если существует функция у=х+z, то это значит, что результат функции (y) зависит от аргументов x и z, и этот аргумент видоизменяется под действием функции x+z, по закону изменения, ею предписываемому. Зная этот закон, можно понять, какова будет функция, как при значениях аргумента в 2 и 20, 86 или 101 – одним словом, при любых аргументах функции. Так, мы сможем вычислить, как быстро будет худеть полный человек, который весит 200 кг или 100 кг (конечно, существует множество переменных, которые по-разному соотносятся между собой, и которые следует учитывать в реальной жизни).  

Функции, описывающие законы изменения одной переменной под воздействием другой, бывают разные. Часть из них называется линейными, другая – нелинейными. Сама функция – это описание закона, по которому изменяется скорость движения функции. Так, например, сначала функция синусоиды движется на увеличение, затем на уменьшение, как и функция нормального распределения. Таким образом, скорость не всегда описывается законом «чем больше, тем больше» или «чем меньше, тем меньше». Однако даже такая функция будет считаться линейной, поскольку одна ее часть пропорциональна второй части и действует по принципу качелей – если с одной стороны она поднимается на определенную высоту, то на второй стороне она опускается или поднимается на ту же самую высоту. Происходит это потому, что все операции сложения, вычитания, умножения и деления делают числа прирастающими или убывающими равномерно. Неравномерный скачок может произойти в том случае, если какой-то из аргументов функции возводится в степень. Так, третью степень 15553 посчитать сложнее, чем 15553*3. Поэтому все функции со степенью растут очень быстро. Для сравнения:

если мы считаем функцию f = 3x, тогда значения, прирастая на 2, распределяются так: у = 4*3 = 12; у = 6*3 = 18; у = 8*3 = 24; 

если мы считаем функцию f = x², когда значения х прирастают на 2, то значения растут быстрее: у = 4*4 = 16; у = 6*6 = 36; у = 8*8 = 64. Такой рост в математике зовется экспоненциальным.

Так, функция описывает, как ведут себя числа, подпадающие под ее влияние. Скорость изменения этих функций называется производной. Здесь и возникает необходимость разделения линейной и нелинейной функций. Поскольку скорость движения чисел в линейной функции, как мы выяснили, одинакова на всех участках, ее можно посчитать и привести к конкретному значению. Как если машина движется на протяжении пути от населенного пункта Дубки в населенный пункт Сосенки, не сбавляя и не увеличивая скорости, ее скорость можно увидеть на спидометре – она равна 100 км/ч, поскольку дорога ровная и прямая на всем пути. Тогда нет необходимости выяснять дополнительные сведения о том, как быстро машина двигалась – скорость всегда одинакова, т.е. константна. Такая константная или постоянная скорость держится на "спидометре" любой линейной функции. В то же время скорость нелинейной функции изменчива, как если бы водитель машины сбавлял скорость перед каждым поворотом. Такая скорость для квадратичной функции (где один из аргументов возведен в квадрат) описывается линейным уравнением (уравнением без степеней), для функции третьей степени – скорость описывается квадратным уравнением и т.д. Поскольку производная является описанием того, как работает функция, мы можем узнать, где будут располагаться аргументы функции в тот или иной момент времени, на определенном отрезке функции.

Что будет, если мы будем знать только скорость движения функции, но не саму функцию? Т.к. производная отвечает только на вопрос «как», но не «где», то это можно сравнить с движением в закрытой машине, где из всей доступной информации известна только скорость. При этом у водителя нет ни малейшего представления, где он находится. Это и есть производная функции. Для того, чтобы понять, каков был путь, т.е. как выглядит функция (зависимость одной величины от другой), необходимо найти первообразную. Это действие противоположно нахождению производной. Следовательно, найти первообразную - значит понять, как выглядела функция, скорость изменения которой нам известна.

Можно сравнить это с мясорубкой. Скорость работы мясорубки – это ее производная. Если мы знаем, что мясорубка перемалывает продукты с определенной скоростью, которая то увеличивается, то уменьшается, то мы можем представить, как выглядит работа этой мясорубки – это будет ее первообразная. Числа же, которые попадают в мясорубку, представляют собой аргументы функции. И нет большой разницы, что будет являться материалом – мясо, вишня или глина – перемалывать мясорубка будет на определенной скорости (производная функции) с определенной величиной элементов фарша (результат функции).

Посчитать интеграл – значит узнать, как вела себя функция на промежутке, где известны только ее производные (ее скорость). По производным производится попытка восстановить изменения функции. Представим, что мы едем по дороге в машине, но машина с педалями. Мы знаем, что ехали по дороге несколько часов, прилагая равные усилия, но ехали то быстрее, то медленнее – где-то в гору, где-то с горы. Чтобы восстановить расстояние (посчитать интеграл), нужно посчитать первообразные от суммы производных (скоростей) на заданном промежутке времени.